
Teorias Rotativas 02
Texto: Renan Montebelo – Vitrine: Eduardo Godoi
Olá amigos do Canal Piloto! Vamos para o nosso segundo artigo sobre Teoria de Voo para Asas Rotativas. O assunto de hoje será o Gráfico Polar do Perfil.
Como você já sabe, o rotor de um helicóptero não é composto por hélices, mas sim por asas. Cada uma das pás do rotor é uma asa que tem a função de gerar Sustentação (S) e Tração (T) para o voo. No entanto, é impossível gerar essas forças sem que seja gerado também um pouco de arrasto (A), que é uma força de resistência (contrária) ao movimento da pá.
As asas são sempre elaboradas de maneira a maximizar a Sustentação ao mesmo tempo que minimizam o Arrasto e isso é possível por terem um perfil afilado e superfícies bem lisas. Antes de continuarmos, segue uma pequena revisão sobre o perfil da asa:
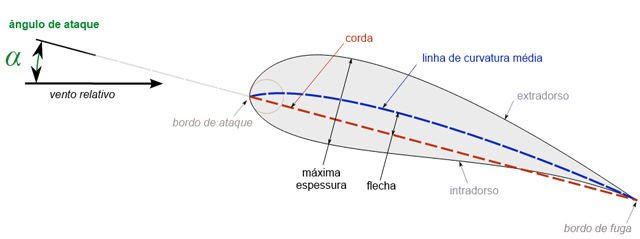
Traduzido de http://en.wikipedia.org/wiki/File:Wing_profile_nomenclature.svg, licença Creative Commons
ü Corda: linha que une o bordo de ataque ao bordo de fuga. Se dividir a asa em exatas duas partes iguais o perfil é simétrico; caso contrário, o perfil é assimétrico (exemplo acima);
ü Linha de curvatura média: linha que divide um perfil assimétrico em duas partes iguais. No caso de perfil simétrico coincide com a corda;
ü Ângulo de ataque: ângulo formado entre a corda e o vento relativo. Pode ser positivo, negativo ou nulo (0º);
Continuando, hoje vamos focar somente na Sustentação e no Arrasto gerados pela asa. As fórmulas dessas duas forças são muito parecidas, como se pode ver abaixo (notar que a velocidade não é diretamente proporcional, pois na fórmula é elevada ao quadrado):
S = Cs * Da * As * Vp2 * ½
A = Ca * Da * As * Vp2 * ½
- S = Sustentação gerada
- Cs = Coeficiente de sustentação
- A = Arrasto gerado
- Ca = Coeficiente de arrasto
- Da = Densidade do ar
- As = Área de superfície da pá
- Vp = Velocidade da pá
O perfil afilado e a superfície lisa da pá permite que o Cs seja o maior possível enquanto o Ca é o menor possível. No entanto, esses valores – que são determinados experimentalmente pelo fabricante da asa – variam com o Ângulo de Ataque (AdA).
Quando um helicóptero decola é necessário que a sua sustentação aumente gradativamente. Vamos analisar através da fórmula acima quais opções o piloto tem para aumentar essa sustentação: a ‘Da’ não é uma opção pois o piloto não tem controle sobre a densidade do ar;
A ‘As’ também não é uma opção, pois a área da pá não muda; a ‘Vp’ seria uma boa opção aumentando a velocidade de rotação das pás, mas por questões que discutiremos em próximos artigos esta deve se manter praticamente fixa durante todo o tempo de voo. Ora, então a única maneira que resta para o piloto aumentar a sustentação é aumentando o ‘Cs’, que como vimos varia com o ‘AdA’!
O ‘AdA’ das pás sofre influência do vento relativo (subidas, descidas, inclinação do rotor) e também da inclinação da corda, que ocorre quando mudamos o ângulo de passo das pás do rotor com os comandos coletivo e/ou cíclico. Então podemos dizer que, basicamente, o piloto controla a sustentação e o arrasto através do ângulo de passo das pás.
Ao aumentarmos o ângulo de passo, aumenta-se a sustentação e também o arrasto, mas existe um limite que precisa ser observado. Portanto, é muito importante observarmos o Gráfico Polar do Perfil da asa, que nos mostra claramente a relação do ângulo de ataque com a sustentação (S) e arrasto (A) gerados:
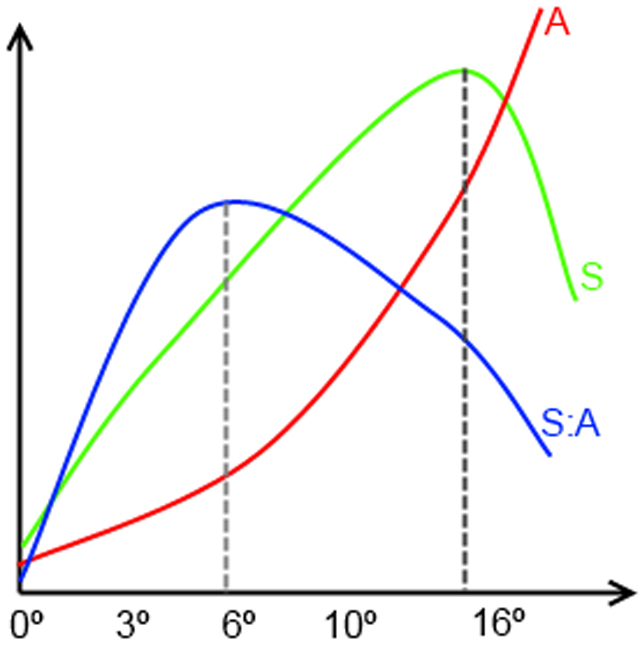
Gráfico elaborado por mim, licença Creative Commons. Valores dos ângulos fictícios; gráfico sem escala
No gráfico de exemplo acima (o gráfico e os valores dos ângulos variam conforme o aerofólio) vemos que a linha verde (Sustentação) aumenta conforme o ângulo de ataque aumenta até aproximadamente 15º. Se aumentarmos ainda mais o ângulo ocorrerá uma queda brusca da sustentação. Esse ângulo (nesse exemplo, 15º) é conhecido como Ângulo Crítico, Ângulo de estol ou Ângulo de Máxima Sustentação.
Essa queda brusca com ângulos maiores que o crítico ocorre porque o vento relativo sofre um desvio tão grande no extradorso que acaba se “descolando” da asa e turbilhonando. O ângulo crítico gera muita sustentação, mas também gera muito arrasto. Nessas condições o motor do helicóptero é muito exigido, e por esse motivo essa situação deve ser evitada sempre que possível.
Geralmente esse ângulo é usado em Decolagens de Máxima Performance, para que o helicóptero ganhe altitude rapidamente e livre obstáculos que não podem ser evitados (prédios, morros, etc).
A linha vermelha representa o arrasto gerado. Este sempre aumenta quanto maior o ângulo de ataque, e aumenta mais rapidamente em ângulos maiores. Por isso é importante observarmos a linha azul: esta é a relação (divisão, razão) entre sustentação gerada e o arrasto gerado e é chamada de eficácia do perfil.
Linha azul = Eficácia do Perfil = S / A
Obviamente é interessante que essa relação seja a maior possível e verificamos que o máximo valor ocorre aproximadamente aos 6º, onde a linha verde é “mais distante” da linha vermelha. Esse é o Ângulo Ótimo que é utilizado nas auto-rotações pois é preciso gerar sustentação com o menor arrasto possível para que as pás não percam rotação (estamos sem motor, lembra-se?).
Veja que o valor do ângulo ótimo varia de asa para asa, mas nunca ocorre em grandes ângulos de ataque. É discutível a afirmação que sempre ocorre em pequenos ângulos, afinal, podemos considerar 5º ou 6º sendo pequenos ou médios, por isso é importante avaliar todas as questões apresentadas pela ANAC e desconsiderar aquelas que são erradas.
É importante salientar que o helicóptero não tem um instrumento que mede o ângulo de ataque, mas sabe-se que quando os parâmetros de manobra estão de acordo com o recomendado pelo fabricante você está provavelmente utilizando o ângulo de ataque adequado.
No Robinson 22, por exemplo, quando você faz uma auto-rotação mantendo 65kts e tacômetro do rotor no arco verde, você estará utilizando o ângulo ótimo (ou muito próximo deste).
Uma curiosidade: você sabe dizer com certeza olhando apenas para o gráfico polar do perfil acima se o perfil em questão é simétrico ou assimétrico?
Vejamos como a ANAC pode cobrar esse assunto em provas.
Questão 1 – O aumento do coeficiente de sustentação será limitado pelo:
a) Ângulo mínimo;
b) Ponto de perda;
c) Ângulo de estol;
d) Ponto de sustentação nula;
Questão 2 – O ângulo da corda do perfil de um aerofólio e o vento relativo chama-se ângulo:
a) de incidência;
b) crítico;
c) de flecha;
d) de ataque;
Questão 3 – A relação entre sustentação e resistência ao avanço de um perfil dá-se o nome de:
a) coeficiente de sustentação;
b) polar do perfil;
c) eficácia do perfil;
d) ângulo ótimo;
Questão 4 – A melhor razão de sustentação e arrasto verifica-se:
a) a grandes ângulos de ataque;
b) no passo mínimo;
c)em altas velocidades;
d) a pequenos ângulos de ataque;
Questão 5 – O coeficiente de sustentação é máximo:
a) no ângulo de sustentação nula;
b) no ângulo ótimo;
c) no ângulo de estol;
d) na velocidade máximo alcance;
Questão 6 – O gráfico que representa as características de um perfil de asa é:
Obs.: Cl = Coeficiente Lift (Sustentação) / Cd = Coeficiente Drag (Arrasto)
a) gráfico Cl / Cd;
b) eficácia do perfil;
c) gráfico de ângulo de ataque;
d) gráfico polar do perfil;
Questão 7 – O arrasto não é diretamente proporcional à:
Obs.: lembrar que na fórmula a velocidade é quadraticamente proporcional, não é diretamente proporcional.
a) densidade do ar;
b) velocidade da pá;
c) área da superfície da pá;
d) coeficiente de arrasto;
Questão 8 – O fator de cálculo do arrasto que depende do formato do aerofólio e do ângulo de ataque é o:
a) densidade;
b) área de superfície;
c) velocidade;
d) coeficiente de arrasto;
Questão 9 – Quando a asa atinge o ângulo de ataque crítico ocorre:
Obs.: checar gráfico polar do perfil em caso de dúvida.
a) CL Máximo e CL Mínimo;
b) CD mínimo e CD alto;
c) CL Máximo e CD Alto;
d) CL Mínimo e CD Mínimo;
Questão 10 – Em uma decolagem normal onde o helicóptero “corre” a pista para ganhar velocidade antes de ganhar altura podemos afirmar que está sendo usado um ângulo de ataque:
a) Próximo ao ângulo ótimo;
b) Próximo ao ângulo crítico;
c) Maior que o ângulo crítico;
d) Nulo;
Respostas: 1c, 2d, 3c, 4d, 5c, 6d, 7b, 8d, 9c, 10a.
Obs. curiosidade: o gráfico polar apresentado é de um perfil assimétrico porque com 0º de ângulo de ataque está sendo gerada uma pequena sustentação.
Por hoje é só, espero que tenham gostado do artigo.
Bons voos à todos.
Renan Montebelo
renanpolo@gmail.com
